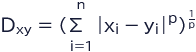ITP1_10_D ミンコフスキー距離をC++で解いてみた[AIZU ONLINE JUDGE]

こんにちは！ mnbd（@mnbbbbbd）です。

AIZU ONLINE JUDGEの「ITP1_10_D ミンコフスキー距離」を解いてみましたので、その回答と解説をご紹介いたします。

プログラミング初心者なので、もっといい回答があるに違いありません。

あくまでも「動作はする」サンプルとしてご覧ください。

問題文
解答
ハマったポイント
まとめ

問題文

２つのデータがどれだけ似ているかを、それらの距離で測る手法は、クラスタリングや分類など、様々なところで使われています。
ここでは、２つの nn 次元ベクトル x={x1,x2,…,xn}と y={y1,y2,…,yn}の距離を計算してみましょう。
このようなデータの距離を測る指標のひとつとして、次のミンコフスキー距離が知られています。
p=1 のとき
となり、これはマンハッタン距離とよばれます。
p=2 のとき
となり、これは一般的に使われるユークリッド距離になります。
p=∞ のとき
となり、これはチェビシェフ距離と呼ばれます。
２つの n 次元ベクトルが与えられるので、p がそれぞれ 1、2、3、∞ のミンコフスキー距離を求めるプログラムを作成してください。
Input
１行目に整数 n が与えられます。２行目にベクトル x の要素 {x1,x2,…xn}、３行目にベクトル y の要素 {y1,y2,…yn} が空白区切りで与えられます。入力はすべて整数値です。
Output
p がそれぞれ 1、2、3、∞ の順番にそれぞれ１行に距離を出力してください。ただし、0.00001 以下の誤差があってもよいものとします。
Constraints
1≤n≤100
0≤xi,yi≤1000
https://onlinejudge.u-aizu.ac.jp/courses/lesson/2/ITP1/10/ITP1_10_D

解答

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n;
    cin >> n;
    int x[n];
    int y[n];
    for(int i = 0; i < n; i++) {
        cin >> x[i];
    }
    for(int i = 0; i < n; i++) {
        cin >> y[i];
    }

    for(int p = 1; p <= 3; p++) {
        double ans = 0;
        for(int i = 0; i < n; i++) {
            ans += pow(fabs(x[i] - y[i]), p);
        }
        cout << fixed << pow(ans, 1.0 / p) << endl;
    }
    double ans = 0;
    for(int i = 0; i < n; i++) {
        if(ans < fabs(x[i] - y[i])) {
            ans = fabs(x[i] - y[i]);
        }
    }
    cout << fixed << fixed << ans << endl;

    return 0;
}